Hello!
My name is Steve Bronder, I am a software engineer at the Flatiron Institute (Simons Foundation) working with Dr Fruzsina Agocs (Department of Computer Science, CU Boulder).
I would like to contribute a new ODE solver for the solution of second order, linear, homogeneous ordinary differential equations (ODEs) with potentially rapidly oscillating solutions to SciPy. The problems the proposed method is able to solve are initial value problems (IVPs) of the form
We built a header-only C++ library and a Python package called riccaticpp implementing the numerical method described in [1] for solving
these problems. We would like to integrate these methods into the scipy.integrate module.
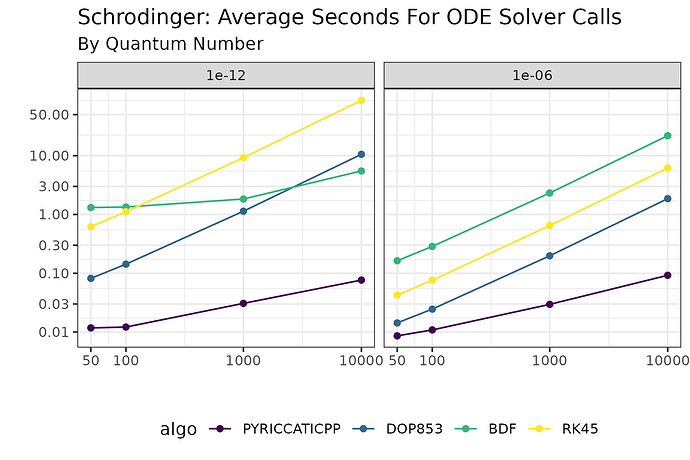
The runtime of methods for oscillatory IVPs currently available in SciPy scales proportionally to \omega, the frequency of oscillations in the solution, which gets prohibitively slow for large \omega. Problems such as in the form above, however, frequently appear in physics simulations (e.g. in quantum mechanics, electric circuits, suspension systems, molecular dynamics, cosmological models), and are a computational bottleneck. The method we propose is efficient: in the worst case, it performs similarly to the high-order explicit methods in scipy.integrate.solve_ivp, but under certain conditions, its runtime is frequency- (\omega-)independent.
Giving researchers easy access to this general purpose solver for oscillatory ODEs via SciPy will allow them to explore more computationally complex models in their research and speed up existing implementations.
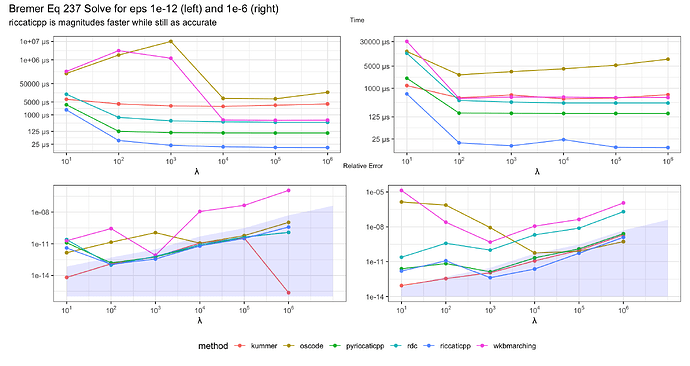
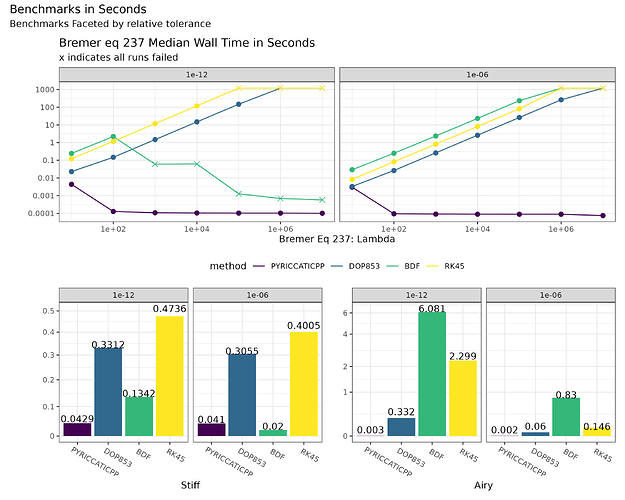
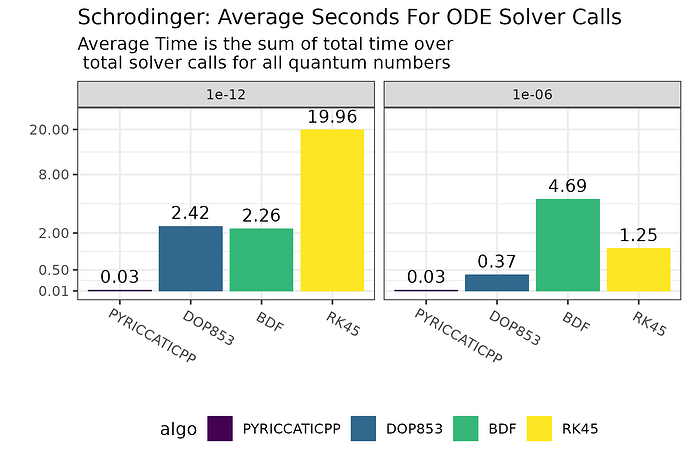
riccaticpp outperforms existing oscillatory solvers for examples such Bremer’s equation 237 below with a runtime that is faster by a a factor of 2 to 100. the graph below compares the runtimes of state-of-the-art solvers and riccaticpp on the test problem
with q(t) = \sqrt{1 - t^2\cos (3 t)}. The solution of this test problem oscillates with a time-dependent frequency \approx \lambda, chosen because some of the methods under comparison can only handle a less general class of IVPs whose solution is always oscillatory. riccaticpp can handle ``turning points’’ in the solution, i.e. regions of no or slow oscillation.
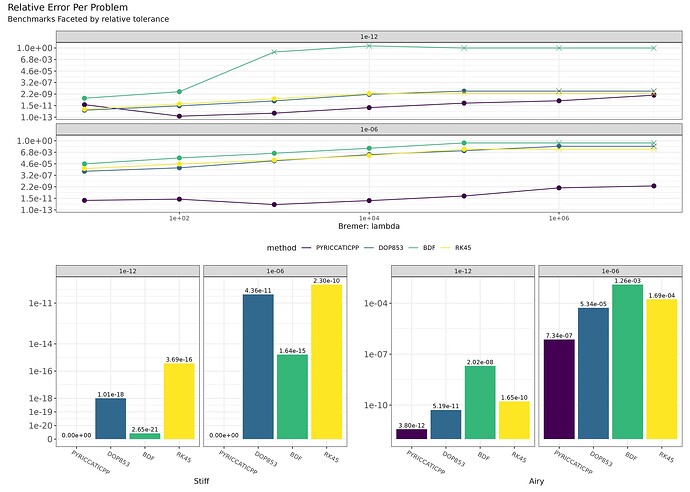
The top two graphs show the median run time for epsilon equal to 1e-12 and 1e-6 while the bottom two graphs show the error of the last point relative to Bremers solutions. The blue area in the graph of errors is the best possible lower bound for error calculated by Bremer. Because the results of each algorithm are compared relative to Bremer’s values, the algorithms may report smaller values than the actual possible error, but should be considered bounded by the blue area.
The current C++ build is based on cmake, but I would be happy to move things over to meson. Our only C++ dependency is the Eigen library. We use c++17, but the code could be made c++14 compliant if preferred.
The current Python API first builds an opaque block for holding precomputed quantities for a given problem that may then be reused in repeated solves (e.g. a grid search). It also holds an arena allocator whose memory is reused between and within solves. Below is an example of users calling the package for solving Bremers equation. We would be happy to modify this API to make it look more similar to those of the current SciPy solvers where possible.
import pyriccaticpp as ric
import numpy as np
import scipy.special as sp
epss, epshs, init_step = [1e-12, 1e-6], [1e-13, 1e-9], [35, 20], [0.1, 0.01, 1e-3]
for lambda in np.logspace(1, 7, num=7):
omega = lambda t: lambda * np.sqrt(1 - t**2 * np.cos(3 * t))
gamma = lambda t: np.zeros_like(t)
info = ric.Init(omega, gamma, 8, 32, 32, 32)
t0 = 1e0
tn = 1e6
u0 = complex(sp.airy(-xi)[0] + 1j * sp.airy(-xi)[2])
du0 = complex(-sp.airy(-xi)[1] - 1j * sp.airy(-xi)[3])
Neval = int(1e2)
t_eval = np.linspace(xf, xi, Neval)
for eps, epsh, in_step in zip(epss, epshs, init_step):
xs, ys, dys, ss, ps, stypes, yeval, dyeval = ric.evolve(
info, t0, tn, u0, du0, eps, epsh, init_stepsize=in_step, x_eval=t_eval
)
Please let us know if integrating this method into SciPy would be of interest and possible. If so, we would love to discuss the integration process and requirements. Thank you for your time!