Hello everyone,
I am a new member and looking for ways to contribute. Currently, I would like to contribute some new code, but will need permission. My code is an extrapolation algorithm based on Taylor Series. While it is not complete, I would still like to see if it can be contributed.
-Thanks
Hi @user-10235 - to which project are you hoping to contribute your code?
Depending on the code you are considering, opening an issue to discuss with maintainers for that project would be the way to go. If you have a concrete implementation already, would you be willing to give more details? In particular, how does your code compare to existing implementations for the same problem, and does it fit the scope of the library you are hoping to contribute to?
Cheers!
Hi,
After looking at the scipy docs approximate_taylor_polynomial, I am unsure whether this function on scipy is designed to approximate a function on the xy-plane, or to graph an unknown function on the xy-plane based on the points on that plane, or even both. My code is based on those points to make an accurate prediction of the graph, but uses a lot of digits and sometimes takes a few seconds to compute.
Additionally, there are extrapolation algorithms in scipy, but they are not based on Taylor Series, since their do not names seem to match with it. My guess is that they are not, because the my code can handle large digits.
I am also unsure where to start, so looking at the link above would give you an idea of what I am looking at, because the code may already exist in scipy. If it already does, please give me an idea of what I can start contributing to.
-Thanks again
approximate_tailor_polynomial is a dusty corner of scipy.interpolate.
If this function were proposed now, I doubt we’d accept it, in its current form at least. I’d say it’s better to replicate it with a newer np.polynomial framework instead of np.poly1d.
Since it’s just a few lines of code, and the main non-algorithmic content here is the choice of breakpoints (Chebyshev nodes look reasonable for a general-purpose library but in specific use cases one can probably do better), it seems appropriate to just do it in the userland.
Regardless, could you explain in some more detail what is the functionality you are proposing?
the code may already exist in scipy
If you mean extrapolation, there’s not much.
Piecewise polynomials extrapolate from the first and last pieces, whatever they are. These extrapolations are useless more often than not.
There’s new rational function algorithms in scipy 1.15, AAA and FloaterHormannInterpolator, these also do not use Taylor expansions either.
The functionality of my code is to take an interval of points that align with a curved line and predict the plot of a function on an interval multiple times the size of the first interval. In order to make an accurate prediction, the number of digits will need to be large and there need to be a lot of points to make the prediction out of. Also, the program fails to make predictions if the points on the interval do not align with a curve (having sharp turns).
To give you a perspective of the capability of the code, I used it to plot a function about 15X the size of its interval. The approximation of the function (red) took little less than 3 seconds to compute on the interval of points (blue).
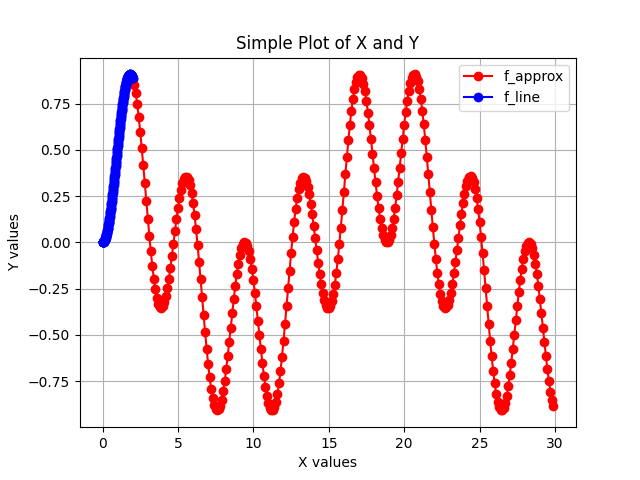
Perhaps in the future, the code can be improved to include a regression algorithm and remove any sharp turns.
Thanks for the demonstration! Is there a reference for the approach you’re using? In SciPy, we typically tend to include well-established algorithms which are widely used. A reference with a large citation count is one way to show a wide use—of course, it’s not the only way, and if you’ve an alternative metrics to argue it’s widely used, then great, please let us know.
If it’s an original R&D, we might want to let it mature as a separate PyPI package first.
Cheers,
Evgeni
I do not think it is a widely used algorithm, since I did not find much about it. I only found this article Mathematical Construction of Interpolation and Extrapolation Function by Taylor Polynomials. I think it is more of an R&D since I did not find something that is a good match. However, I think this article might have the mathematics of the algorithm but I will need to look at it more closely and check again for something I might have missed.
Other than that, I have not seen it anywhere else. In case you need to see the code let me know so I can publish it on my github. It is not quite done and needs additional work.